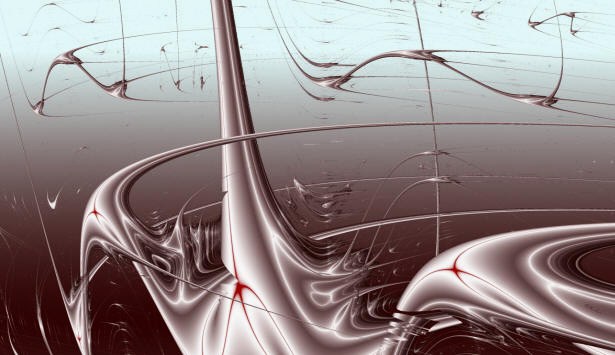
Die Mathematik hat schon immer Bilder geliefert, z.B. solche geometrischer Objekte oder der Graphen von Funktionen. Künstlerisch bietet sich da aber wenig Gestaltungsspielraum. Geändert hat sich das mit dem Aufkommen der Chaostheorie und der fraktalen Mathematik. Fraktale Kunst berechnet und gestaltet mit Hilfe des Computers vorwiegend Strukturen aus den mathematischen Bereichen Fraktale Geometrie, Mandelbrotmenge (Apfelmännchen) und Juliamengen. Kaum bekannt sind hingegen die auf Professor Mario Markus zurückgehenden Ljapunow-Diagramme. MatheKunst hat das Anliegen, diesen auf dem Kunstmarkt mehr Aufmerksamkeit zu verschaffen, zumal hier ein weit größerer Fundus möglicher Strukturen vorliegt als bei den mathematisch einfach zu handhabenden Mandelbrot- und Juliamengen.
Hintergrund ist die iterative Berechnung dynamischer Prozesse. Alles in unserer Welt, was sich in der Zeit verändert, gilt als dynamischer Prozess, gleichgültig ob dies nun dem Bereich der Naturwissenschaften, Gesellschaftswissenschaften, Geisteswissenschaften oder Wirtschaftswissenschaften zuzuordnen ist. Iterative Berechnung bedeutet, dass man aus dem Anfangszustand eines Systems die Folgezustände durch wiederholte (iterierte) Anwendung derselben Funktion erhält. Als Beispiel kann man das Wachstum einer Population betrachten, deren Individuenzahl sich von einem Zeitpunkt zum nächsten jeweils durch Anwendung der logistischen Gleichung berechnet. Dies ist ein ordentlicher Vorgang in dem Sinne, dass zwei Populationen, deren Anfangswerte dicht beieinanderliegen, auch später noch sich nicht wesentlich unterscheiden werden. Hängt der Vorgang nun von einem Parameter ab, wie z.B. der Temperatur in einer Bakterienkultur, so kann der Vorgang chaotisch werden, wenn dieser Parameter in einem bestimmten Rhythmus zwischen zwei Zahlen x und y zwangsweise gewechselt wird. Chaotisch heißt hier, dass zwei Populationen mit dicht beieinanderliegenden Anfangswerten sich bei gleichen Bedingungen nach einiger Zeit sehr unterschiedlich entwickeln werden.
Der russische Mathematiker A. M. Ljapunow (1857-1918) hat als "Begründer der Theorie der Bewegungsstabilität" (Grabinschrift) ein Verfahren entwickelt, das eine Beurteilung erlaubt, in welchem Ausmaße sich ein dynamisches System ordentlich oder chaotisch verhält, wenn ein Parameter in diesem System gezwungen wird, zwischen zwei Zahlen x und y nach einem bestimmten periodischen Muster zu wechseln. Dieses Verfahren liefert zu jedem solchen Zahlenpaar (x, y) eine Zahl, die üblicherweise mit dem griechischen Buchstaben Lambda bezeichnet wird und auch Ljapunow-Exponent heißt. Ist Lambda positiv, verhält sich das System chaotisch, bei negativem Lambda ordentlich. Jedes Zahlenpaar (x, y) kann als Punkt in einer Ebene mit 2 Koordinatenachsen gedeutet werden. Geht man nun von diesem Punkt (x, y) aus bei positivem Lambda um den Betrag von Lambda senkrecht nach oben oder bei negativem Lambda um den Betrag von Lambda senkrecht nach unten, so erhält man einen durch das Zahlentripel (x, y, Lambda) eindeutig bestimmten Punkt im dreidimensionalen Raum. Berechnet man nun für jedes Zahlenpaar (x, y) in einem zum Beispiel rechteckigen Bereich der Koordinatenebene die jeweilige Zahl Lambda, so bildet die Menge aller Punkte zu den Zahlentripeln (x, y, Lambda) eine irgendwie geformte Fläche im Raum über bzw. unter dem rechteckigen Bereich in der x-y-Ebene.
Diese Situation ist vergleichbar mit einem rechteckigen Bereich der Erdoberfläche. Lässt man zunächst die Höhenunterschiede weg, so wird jeder Punkt in diesem rechteckigen Bereich durch die zwei Zahlen geografische Länge und geografische Breite festgelegt. Zu jedem Zahlenpaar (Länge, Breite) gehört nun eine Zahl "Höhe", die angibt, um wieviele Meter der entsprechende Punkt der Erdoberfläche sich über oder unter dem Meeresniveau befindet. Die Menge aller Punkte zu den Zahlentripeln (Länge, Breite, Höhe) bildet dann also die Erdoberfläche als räumliches Objekt.
Aus einem rechteckigen Bereich des räumlichen Objektes "Erdoberfläche" macht man ein ebenes Bild, also eine topografische Karte, indem man jedem Zahlenpaar (Länge, Breite) in Abhängigkeit von der Höhe eine Farbe zuordnet. Mit zunehmender positiver Höhe geht man z.B. von einem dunklen Grün für die Niederungen über heller werdende Grüntöne zu hellem Braun und kommt schließlich zu dunklem Braun für die höchsten Erhebungen. Für negative Höhen, also den Meeresboden, kommt man von Hellblau für das Flachwasser bis zu dunklem Blau für die tiefsten Bereiche des Meeresbodens. Anschließend werden die Berg- und Talflanken noch einer Hell-Dunkel-Gestaltung unterzogen, um durch eine Licht-Schatten-Wirkung einen räumlichen Eindruck zu erhalten.
Ein Ljapunow-Diagramm ist nun nichts weiter als eine topografische Karte der durch die oben genannten Zahlentripel (x, y, Lambda) gebildeten Fläche im Raum. Jedem der oben genannten Zahlenpaare (x, y) wird in Abhängigkeit von Lambda eine Farbe zugeordnet. In dem Ausmaße, wie man die Kunst beherrscht, den Zahlen "Lambda" Farben zuzuordnen, kann aus dem Ljapunow-Diagramm ein Kunstwerk werden.
zurück zu Die Mathematik | zurück zum Anfang
Am Anfang steht die Wahl einer geeigneten Iterationsfunktion und eines rechteckigen Ausschnitts der x-y-Ebene. Um ein Ljapunow-Diagramm im Format DIN A1 zu entwickeln, wird dieses Rechteck durch 11353 x 7852 = 89143756 Punkte repräsentiert und zu jedem Punkt (x, y) der Ljapunow-Exponent Lambda berechnet. Für dieses Zahlenfeld aller Lambda-Werte werden 850 MByte Arbeitsspeicher benötigt. Zur Berechnung eines einzigen Wertes Lambda werden je nach gewünschten Eigenschaften des Bildes 1000 bis 20000 Iterationsschritte, d.h. Funktionswertberechnungen durchgeführt. Für das Zahlenfeld aller Lambda benötigt ein Prozessor mit 3,2 GHz gegenwärtig (2011) meist eine Rechenzeit von 2 bis 5 Tagen. Als ich 1995 anfing, Ljapunow-Diagramme zu berechnen, hat mein damaliger Rechner schon für das kleine Format DIN A3 zwei bis drei Wochen gerechnet.
Jeder der 11353 x 7852 Punkte (x, y) ist ein Punkt des Bildes und wird entsprechend dem zugehörigen Wert von Lambda eingefärbt. Entscheidend für die Möglichkeiten künstlerischer Gestaltung ist nun das im Programm bereitgestellte Instrumentarium, mit dem den Zahlen Lambda auf vielfältige Weise Farben zugeordnet werden können. Dazu wird zunächst eine statistische Graphik erstellt, aus der ersichtlich wird, welche Zahlenwerte für Lambda überhaupt vorkommen. Der Zuordnungsprozess zwischen den Zahlen und den Farben wird dann rein mathematisch durch auswählbare und transformierbare Funktionen bewerkstelligt, da dies wegen der Millionen unterschiedlicher vorkommender Zahlen und eines Farbraumes mit 16 Millionen Farben nicht sozusagen einzeln von Hand für jede Zahl festgelegt werden könnte. Dazu wird die Gesamtheit aller Potenz- und Wurzelfunktionen zur Auswahl bereitgehalten. Mit diesen wird folgendes jeweils separat gesteuert :
Ferner kann der Punkt des Überganges zwischen Vorder- und Hintergrund verschoben sowie der Hintergrund von Lambda entkoppelt und separat durch mathematische Strukturen gestaltet werden. Dies kann sich unter künstlerischen Gesichtspunkten als wünschenswert erweisen, da der Hintergrund als Bereich des Chaos von den Lambda-Werten her meist wenig strukturiert und damit auch wenig gestaltbar ist.
Der ursprünglich gewählte rechteckige Ausschnitt der in alle Richtungen unendlich ausgedehnten x-y-Ebene ist nun irgendein Bild - das aber noch lange nicht gefallen muss. Daher ist es nun möglich, darin wiederholt einen formvariablen Ausschnitt zu wählen und auf ein Rechteck und die ursprüngliche Größe umzurechnen, bis man ein inspirierendes Motiv gefunden hat. In die unendlich große x-y-Ebene kann man auf der Suche nach Bildern also auch unendlich tief hineinzoomen. Interessant ist an vielen Bildern, dass im Bereich der Ordnung (Vordergrund) scharfe Schnitte, Durchbrüche, Unschärfen und Einbrüche des Chaos auftreten, welche die Vollkommenheit der Ordnung und der scheinbaren Symmetrien stören. Dies ist ein wesentlicher Charakter dieser dynamischen Systeme und damit auch der Natur.
Das Bild mit 11353 x 7852 Punkten ergibt bei 360 dpi das Format DIN A1 und benötigt 255 MByte Speicher. Für eine feinere Auflösung und Druckqualität mit 720 dpi wird für den Druckvorgang die Zahl der Punkte durch Interpolation noch vervierfacht, so dass dabei dann 1 GByte an Daten verarbeitet wird. Das von mir geschriebene Delphi-Programm umfasst 1630 Zeilen zu je durchschnittlich 100 Zeichen.
zurück zu Die Mathematik | zurück zum Anfang
Diese Frage wird oft gestellt. Aus den Erläuterungen zum Programm ergibt sich, dass nicht etwa ein von vornherein durch die Mathematik festgelegtes Produkt erzeugt wird. Der Künstler begibt sich hier zunächst in einem unendlichen Raum auf die Suche nach einem Motiv, so wie es etwa auch der Kunstfotograf tut. Dann gestaltet er das Motiv mit einem breiten mathematischen Instrumentarium, welches ihm weit mehr Gestaltungsmöglichkeiten bietet, als der Fotograf sie hat. Gleichwohl hat der Gestaltungsvorgang Beschränkungen durch die Struktur "Feld der Zahlenwerte Lambda" und die Möglichkeiten des Instrumentes "Programm". Dies ist vergleichbar mit einem Komponisten, der sich mit der Struktur "Quartett" und den Instrumenten "Oboe, Violine, Viola und Violincello" befasst. Wie vielfältig die Gestaltungsmöglichkeiten bei der Herstellung der Ljapunow-Diagramme sind, zeigen exemplarisch z.B. die beiden nachfolgenden Bilder , denen jeweils dasselbe Feld von Lambda-Werten zugrundeliegt, die aber dennoch infolge der künstlerischen Gestaltung in eindrucksvoller Weise unterschiedlich ausfallen. Die gemeinsame Grundstruktur lässt sich noch erkennen, wenn man eines der Bilder um 180° dreht.
Wer da meint, Computer und Drucker würden einfach nur mit technischer Präzision eine vorgegebene mathematische Struktur ausgeben, liegt daher genauso falsch wie jemand, der meint, Rembrandt oder Monet hätten nur handwerklich perfekte Kopien einer vorgegebenen Wirklichkeit erstellt.
Neu gegenüber der herkömmlichen Kunst ist, neben den aus den dynamischen Prozessen abgeleiteten Strukturen, die der Mathematik und der Technik gedankte Präzision der Linienführung und die Reinheit, Stetigkeit und Differenzierbarkeit der Farbübergänge, wie keine menschliche Hand und kein menschliches Auge sie je erschaffen könnte. Die Entwicklung der Bilder erfolgt zunächst am Bildschirm durch additive Farbmischung aus Rot-Grün-Blau. Der Druck mit der subtraktiven Farbmischung aus 10 Tinten weicht jedoch vom Aussehen auf dem Bildschirm erheblich ab, so dass in der Regel 10 bis 50 optimierende Probedrucke folgen.
zurück zu Die Kunst | zurück zum Anfang
Ein Kunstlehrer betrachtete meine Bilder, schoss auf eines zu und rief "Oh - Toll - Mozart ! Das will ich haben !" . Wie kann ein Bild mit einer Musik assoziiert werden ?
Eine blühende Wiese in der Sonne oder schroffe Felszacken unter einem düsteren Himmel, der Gesang einer Nachtigall oder das Krächzen eines Raben, eine menschliche Gestalt oder besonders auch der Tonfall einer menschlichen Stimme - Töne und Tonfolgen finden gleichermaßen Eingang in die Welt unserer Gefühle wie Farben und Formen. Das Spiel mit den Gefühlen zu Farben und Formen führt zu Bildern, das Spiel mit den Gefühlen zu Tönen und Tonfolgen zur Musik. So haben wir die Welt unserer Gefühle als eine gemeinsame Wurzel für Kunst und Musik.
Bei jedem Spiel ist der Verstand mit dabei - in der Musik wesentlich auch in Form von Mathematik. Physikalische und mathematische Überlegungen führen im Zusammenspiel mit dem Tonempfinden zu Tonleitern und machen die Musik damit notierbar und reproduzierbar. Rhythmische Elemente werden durch Zahlenverhältnisse angegeben. Das Notenbild vieler Kompositionen weist Elemente geometrischer Operationen auf: Verschiebungen und Spiegelungen ergeben Wiederholungen und Symmetrien, Streckungen und Stauchungen ergeben Ähnlichkeiten.
Auch die Grundstruktur meiner Bilder, die Ljapunow-Diagramme, sind Mathematik. Bei der Ausgestaltung dieser Bilder bediene ich mich statt des Stiftes oder Pinsels wiederum der Mathematik. Als Resultat finden sich in meinen Bildern wie in der Musik Wiederholungen, Symmetrien und Ähnlichkeiten.
Es gibt allerdings einen wesentlichen Unterschied zwischen einer Musik und einem Bild: Musik ist ein flüchtiges Phänomen in der Zeit, ein Bild ist stets in Gänze präsent und ein unveränderlicher Teil des Raumes. Doch diese prinzipielle Trennung in Zeit und Raum ist in Bezug auf meine Bilder, aber auch allgemein, nicht so streng wie es zunächst scheinen könnte.
Eines meiner Bilder im Format DIN A1 enthält Informationen über 300 Millionen Varianten eines dynamischen Prozesses, ist also eine räumliche Manifestation zeitlicher Vorgänge. Schon auf den ersten Blick erwecken diese Bilder ja auch den Eindruck von Dynamik und nicht den eines Stilllebens. Das Auge beginnt beim Betrachten unwillkürlich den Linien und Strukturen zu folgen und macht damit aus dem räumlichen Objekt ein zeitliches Erlebnis wie Musik. Umgekehrt ist die Musik auch nicht ein zeitlich total flüchtiges Phänomen, sondern bleibt in unserem Gedächtnis haften und gewinnt damit eine dauerhafte Präsenz wie ein Bild.
Die Beziehungen zwischen optischen und akustischen Reizen spiegeln sich auch in unserer Sprache wieder: Begriffe wie z.B. "hoch" und "tief", "lang" und "kurz", "leicht" und "schwer", "dunkel" und "hell", "schwinden" und "zunehmen", "konvergieren" und "divergieren" verwenden wir sowohl für Töne und Tonfolgen als auch für Farben und Formen. Seit je her stellt also unser Gehirn Beziehungen her zwischen Bildern und Musik und ordnet darin enthaltene Strukturen in gleiche Kategorien ein.
zurück zu Die Kunst | zurück zum Anfang
Tonfolge mit Verschiebung
nach
rechts ♪♪♪ ♪♪♪
Tonfolge mit Spiegelung an
senkrechter Achse,
eine symmetrische Figur (Musikalisch: Krebsgang)
Tonfolge mit Spiegelung an waagrechter Achse und ♪♪♪ ♪♪♪
Verschiebung nach rechts (Musikalisch: Umkehrung)
Tonfolge mit Spiegelung an senkrechter und ♪♪♪ ♪♪♪
waagrechter Achse (Musikalisch: Krebsumkehr)
Klavierrollennotationen ( senkrechte Achse: Tonhöhe, waagrechte Achse: Zeit ) von Notenschriften machen geometrische Operationen in Kompositionen besonders gut sichtbar, wie die folgenden beiden Beispiele zeigen:
Bild 1 : Verschiebungen in einem Präludium von J. S. Bach
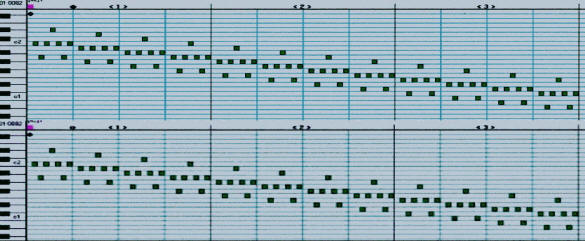
Bild 2 : Symmetrie in einem Krebskanon von J. S. Bach
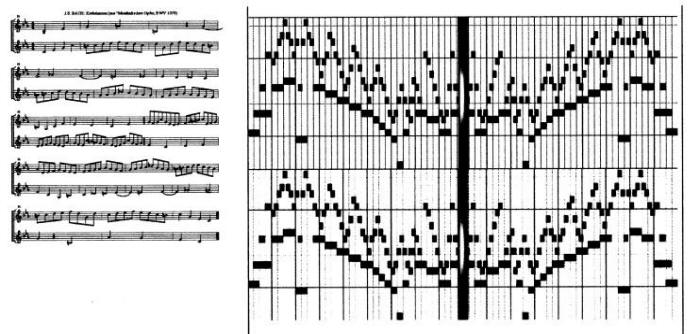
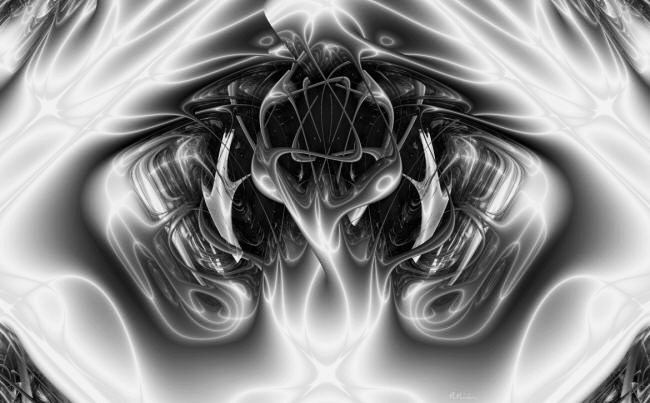
Bild 3 : Mit welcher Berechtigung rief der Kunstlehrer bei der Betrachtung dieses Bildes "Oh - Toll - Mozart" ?
Die Musik von
J. S. Bach als
Bediensteter an absolutistischen Fürstenhöfen und Komponist für strikt
reformatorische Kirchengemeinden ist bei aller barocken Prachtentfaltung und
Kreativität eine an strenge Regeln gebundene Musik - manch kreative und
emotionale Ausbrüche aus diesen Regeln finden bei seinen Auftraggebern wenig
Verständnis (1). Bild 3 ist in seiner barocken Erscheinung
mathematisch geprägt durch Verschiebungen (oben links und rechts an der
Grenze von Hell zu Dunkel sowie mittig links und rechts) und Symmetrie.
Somit finden sich in Bild 3 wesentliche geometrische
Konstruktionsprinzipien, wie sie auch in den Bildern 1 und 2 zu Kompositionen
von J. S. Bach zu sehen sind. Symbolisch für seine Musik ist
sein von ihm selbst entworfenes Siegel (Bild 4), das die Initialien JSB
mitsamt deren Spiegelung enthält und geprägt ist durch Verschiebungen,
Drehungen und perfekte Symmetrie. Warum also zu Bild 3 nicht
der Kommentar "Oh - Toll - Bach !" ?
Obwohl eingebunden in Verschiebungen und Symmetrien,
gewinnt die Mitte von Bild 3 (oder Variante Bild 5) einen eigenständigen,
schwebend leichten, melodiehaften Charakter ohne das im Barock verbreitete
Fortspinnungsmotiv (2). Übertragen in die Musik wird der
barock-polyphone Stil, entsprechend dem Bildrand mit verschiedenen
Serien von gleichberechtigten Verschiebungen, hier verschmolzen mit dem
klassisch homophonen Stil, entsprechend der Bildmitte. Damit kommt man
von Bach zu Mozart (3), vom Genie
in der eingeengten Welt eines Angestellten zum meist freiberuflich arbeitenden
Genie (1)(3). Im Übrigen hat das Barock trotz der Beispiele bei Bach
die Symmetrie bei Motiven eher gescheut, im Gegensatz zur Klassik bei
Mozart (2).
Natürlich kann das zufällige Zusammentreffen
eines Kunstlehrers und Mozart-Liebhabers mit einem
MatheKunst-Bild nicht mehr ergeben als einen eher pauschalen Diskurs über
die Verwandtschaft des Bildes mit Mozart, zumal Mozarts Werk
sehr vielfältig ist. Genauso gut könnte man andere Komponisten zum Vergleich
heranziehen, wobei allerdings die schwebend leichte Struktur des Bildes von
vornherein eine Verwandtschaft mit einer großen Zahl Mozartscher Kompositionen
nahelegt. Wenn man aber andere Komponisten sucht, dann müsste man das wohl in
der Zeit von Barock und Klassik tun, denn schon in der Romantik beginnt das
Überschreiten struktureller Grenzen zugunsten des emotionalen und
programmatischen Inhalts, also eine Auflösung der strengen Form (4).
Nimmt man zum Beispiel den Jazz, so scheidet dieser im Vergleich mit der
europäischen "Konzertmusik der großen Form" wohl von vornherein aus (5).
Die Kompositionen im Jazz sind eher einfach, die Form ist weitgehend eine
lineare Abfolge kleiner Einheiten (Improvisationen) mit grundsätzlich offenem
Ende (5). Das passt in keiner Weise zusammen mit der komplex
zusammenhängenden, in sich geschlossenen dreidimensionalen Welt von Bild 3 oder
Bild 5.
Quellen:
Bild 1:
http://optimierung.mathematik.uni-kl.de/~nchrist/MAMUSI/1geometrie_und_musik.htm
Bild 2:
http://optimierung.mathematik.uni-kl.de/~nchrist/MAMUSI/1geometrie_und_musik.htm
Bild 3: Andreas Heinzelmann, Bild-Nr. 11-0001-008
Bild 4:
http://de.wikipedia.org/wiki/Johann_Sebastian_Bach
Bild 5: Andreas Heinzelmann, Bild-Nr. 11-0001-005
(1):
http://de.wikipedia.org/wiki/Johann_Sebastian_Bach
(2):
http://de.wikipedia.org/wiki/Motiv_(Musik)
(3):
http://de.wikipedia.org/wiki/Wolfgang_Amadeus_Mozart
(4):
http://de.wikipedia.org/wiki/Epoche_(Musik)
(5):
http://de.wikipedia.org/wiki/Jazz
zurück zu Die Kunst | zurück zum Anfang
Das Aussehen der Bilder auf dem
Bildschirm weicht meist deutlich ab von den gedruckten Versionen. Dies liegt zum
einen an den unterschiedlichen Farbsystemen ( Monitore: additive Farbmischung
aus rot, grün und blau; Drucker: subtraktive Farbmischung aus diversen Tinten
auf der Basis von cyan, magenta und gelb ). Zum andern hängt das Aussehen der
Bilder aber vor allem (und vom Verfasser dieser Webseite nicht beeinflussbar)
auch von den Monitoreinstellungen des Betrachters der Webseite ab ( Helligkeit,
Kontrast, Farbintensität ).
Wenn der Betrachter sich Bilder aus dieser Galerie
selbst druckt, werden diese Drucke aus folgenden Gründen von sehr schlechter
Qualität sein und in keiner Weise vergleichbar mit der Spitzenqualität der von
mir verkauften Bilder:
Die Bilder dieser Galerie haben maximal knapp 1
Million berechnete Pixel, meine Bilder im
Format DIN A3+ haben 102 Millionen, im Format DIN A2 169 Millionen und im Format
DIN A1+ 357 Millionen berechnete Pixel.
Die Bilder sind auf meinen
Großformatdrucker mit Spezialpapier und 10 pigmentierten Tinten hin entwickelt
worden und entfalten erst damit ihre einzigartige farbliche Wirkung und ihre
enorme Lebensdauer ( Details siehe
Zertifikat ). Ausdrucke mit anderen Druckern,
Papieren und Tinten weichen von diesem Standard in der Regel erheblich ab.
Wer an meinen
Bildern interessiert ist, kann von mir Probedrucke im Format DIN A4 mit 35
Millionen berechneten Pixeln beziehen. Diese sind allerdings nicht als
Ausstellungsobjekte geeignet ( Details siehe Verkauf ).
Auf die Bestimmungen des Urheberrechts wird
hingewiesen.
Die Bestellnummern der Bilder erscheinen, wenn der
Mauszeiger hier in der kleinformatigen Darstellung auf einem Bild verweilt. Eine
großformatige Darstellung in einem neuen Fenster erhält man durch anklicken des
Bildes, dort ist die Bestellnummer Bestandteil des Bildes.
zurück zu Bilder | zurück zum Anfang
Jedem von mir gedruckten Bild wird ein Zertifikat beigegeben. Dieses gibt an, welche konkreten Materialien der Firma "Epson" verwendet wurden ( Drucker, Pigmenttinten, Papier ) und verweist auf das diesbezügliche Gutachten der Firma "Wilhelm Imaging Research Inc." ( www.wilhelm-research.com ). Nach diesem Gutachten werden für meine Bilder folgende Zeiträume angegeben, in denen keine wahrnehmbaren Farb- oder Papierveränderungen erfolgen: Unter Ausstellungsbedingungen gerahmt hinter Glas 108 Jahre, bei Glas mit UV-Schutz 175 Jahre und unter Archivbedingungen 300 Jahre. Das Zertifikat enthält die Bildbezeichnung, die Ausfertigungsnummer und die maximale Ausfertigungszahl von 200.
zurück zu Bilder | zurück zum Anfang
Bestellungen für Bilder aus meiner Galerie können unter Angabe von Name, Postadresse und Telefonnummer an die EMail-Adresse "MatheKunst@t-online.de" gerichtet werden . Meine Auftragsbestätigung enthält dann die Kontonummer für die Überweisung des Kaufpreises per Vorkasse. Nach Eingang des Kaufpreises wird das Bild von mir innerhalb von 2 bis 3 Wochen versandkostenfrei verschickt.
Ein Bild im Format DIN A3+ ( 483mm x 329mm Papiergröße ) kostet 180 Euro, im Format DIN A2 ( 594mm x 420mm ) 220 Euro und im Format DIN A1+ ( 850mm x 610mm ) 280 Euro.
Gegen einen Betrag von 10 Euro kann auch zunächst eine Prüfversion des Bildes im Format DIN A4 bezogen werden. Diese wird auf demselben Papier, mit denselben Tinten, auf demselben Drucker und mit derselben Auflösung von 720dpi produziert wie die großen Bilder. Diese Prüfversion enthält allerdings, im Gegensatz zu den größeren Formaten, in der Bildmitte in großer Schrift die Bestellnummer und ist daher als Kunst-, Dekorations- oder Ausstellungsobjekt nicht geeignet.
zurück zu Bilder | zurück zum Anfang
Im Hause
MatheKunst
Am Zuckerhut 12
18528 Sehlen
kann gegen telefonische Terminvereinbarung ( 03838 - 4045444 ) gern unverbindlich die Hausausstellung meiner Bilder besucht werden. Verkauf vor Ort ist möglich.
Vom 1.3.2012 bis 12.4.2012 kann eine Ausstellung meiner Bilder in der
Führungsakademie der Bundesagentur für Arbeit
Schützenstr. 50
91207 Lauf
besucht werden. Öffnungszeiten sind Montag bis Freitag von 9 bis 18 Uhr. Verkauf vor Ort ist nicht möglich.
zurück zu Bilder | zurück zum Anfang
Es gibt derzeit mindestens einen Browser, bei dem mit den großen Grafiken im Abschnitt "Geometrie und Musik" Probleme beim Drucken auftreten können. Deshalb ist zu empfehlen, auf jeden Fall zunächst mit den Werkzeugen der Druckvorschau des Browsers ( Hoch-/Querformat, Größe in % ) die zu druckenden Seiten so einzurichten, dass alle Grafiken vollständig und unzerteilt zu sehen sind. Dabei ist es auch möglich, drucktechnisch schwierige Teile der Webseite zu markieren, dann in der Druckvorschau separat zu behandeln ( Einstellung "Wie auf dem Bildschirm ausgewählt" ) und separat zu drucken. Bei geeigneten Einstellungen der Druckvorschau lässt die Webseite sich auf diese Weise bei allen gängigen Browsern einwandfrei drucken.
1944 geboren
in Schlesien
1951 - 1955 Volksschule in Ludwigsburg (Baden-Württemberg)
1955 - 1964 Mörike-Gymnasium in Ludwigsburg
1964 - 1968 Zeitoffizier
der Bundesmarine
1968 - 1977 Studium der Mathematik und Physik an der
Albert-Ludwigs-Universität in Freiburg (Breisgau)
und Mitglied der akademischen Alpinistikgruppe,
Referendar am Kepler-Gymnasium Freiburg,
Assessor am Gymnasium Waldkirch (Schwarzwald)
1974 Heirat, nachfolgend 5 Kinder
1977 - 2009 Fachobmann für
Mathematik und Informatik am
Gymnasium Bad Essen (Landkreis
Osnabrück)
seit 2009 Mathematiker und
Künstler, Segler, Bergwanderer,
Skiläufer,
Jogger, Landschaftsgärtner,
Holzfäller, Opa